树状数组
什么是树状数组(Binary Indexed Tree, BIT)
顾名思义就是一个结构为树形结构的数组,与二叉树的结构类似但又不同,它是在二叉树的结构上删除了一些中间节点。
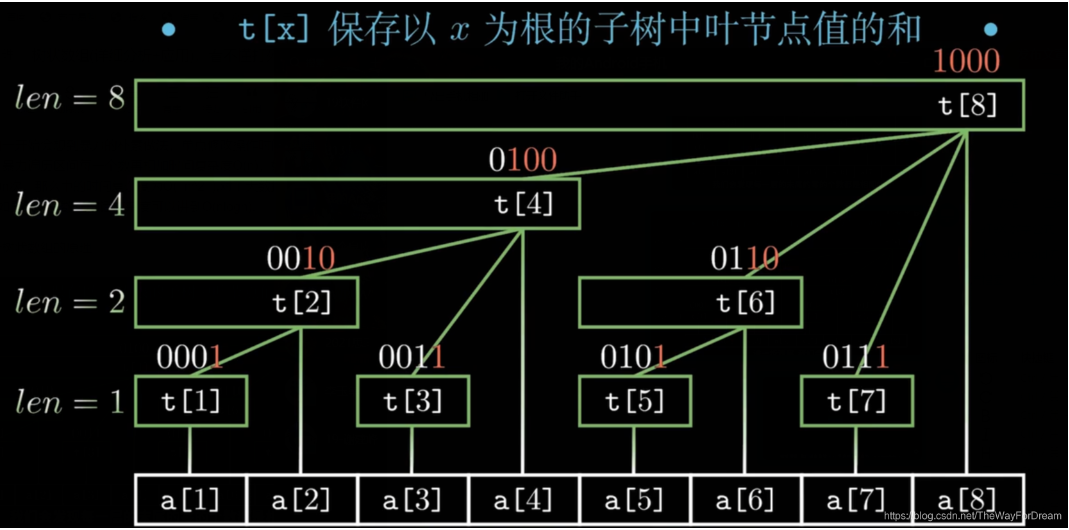
t[x]保存以x为根的子数中叶子节点值的和,原数组为a[]。
它可以解决大部分区间上面的修改以及查询的问题,例如单点修改,单点查询,区间修改,区间查询,换言之,线段树能解决的问题,树状数组大部分也可以,但是并不一定都能解决,因为线段树的扩展性比树状数组要强。
树状数组讲解
lowbit(x)
1 | int lowbit(x){ |
因为是补码,所以该函数可以计算x的二进制表示中最右边的 1 所代表的值。
我们可以发现节点x的父节点为x + lowbit(x)
单点修改
如果我们在单点修改的同时,更新父节点就变得尤为简单。我们要实现a[1]+k,那么t[1],t[2],t[4],t[8]都要 + k;
1 | int add(int x, int k){ |
区间查询
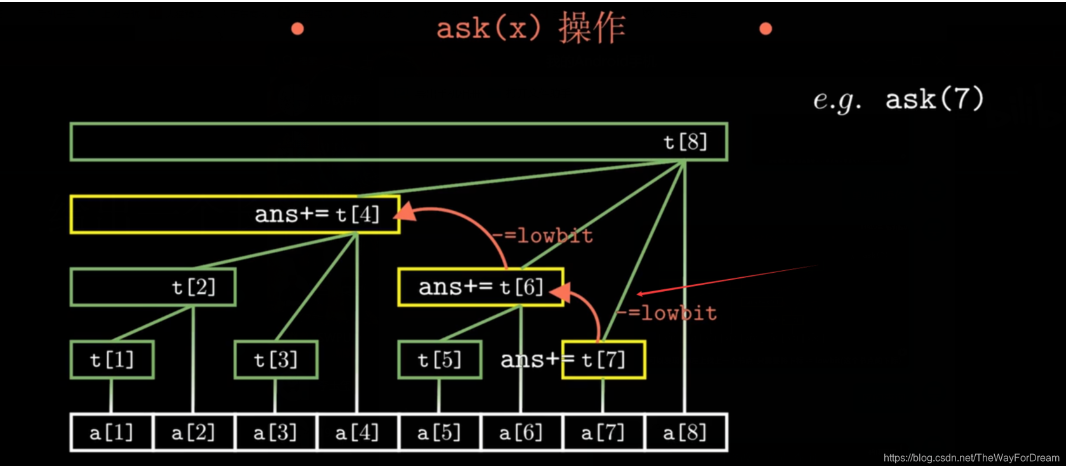
通过图片,可以看到sum[7] = t[7] + t[6] + t[4],6 = 7 - lowbit(7), 4 = 6 - lowbit(6),所以我们可以通过不断的-lowbit()来实现求和。
1 | int ask(int x){ |
这只能求[1, x]的区间和,那么如何求[L, R]的区间和呢,可以利用[L, R] = [1, R] - [1, L - 1]
1 | int search(int L,int R) |
区间修改
对区间[L, R] + k,利用差分数组性质,代码如下:
1 | int update(int x,int k) |
本博客所有文章除特别声明外,均采用 CC BY-NC-SA 4.0 许可协议。转载请注明来源 ing的博客!




